Harmonizing Maximum Likelihood with GANs for Multimodal Conditional Generation

Soochan Lee, Junsoo Ha and Gunhee Kim

ICLR 2019

Abstract

DO NOT USE RECONSTRUCTION LOSS IN CONDITIONAL GANS!

Recent advances in conditional image generation tasks, such as image-to-image translation and image inpainting, are largely accounted to the success of conditional GAN models, which are often optimized by the joint use of the GAN loss with the reconstruction loss. However, we reveal that this training recipe shared by almost all existing methods causes one critical side effect: lack of diversity in output samples. In order to accomplish both training stability and multimodal output generation, we propose novel training schemes with a new set of losses named moment reconstruction losses that simply replace the reconstruction loss. We show that our approach is applicable to any conditional generation tasks by performing thorough experiments on image-to-image translation, super-resolution and image inpainting using Cityscapes and CelebA dataset. Quantitative evaluations also confirm that our methods achieve a great diversity in outputs while retaining or even improving the visual fidelity of generated samples.

Mode Collapse in cGANs

Conditional generation is intrinsically one-to-many mapping. Therefore, a generator is expected to generate diverse outputs for a single input depending on the random noise $z$. However, models based on conditional GAN suffer from serious mode collapse, i.e. end up one-to-one mapping.

For instance, in the image translation task below, the generator should be able to translate a segmentation label to diverse, realistic images. Nonetheless, a conditional GAN trained with the standard training scheme suffers from severe mode collapse.

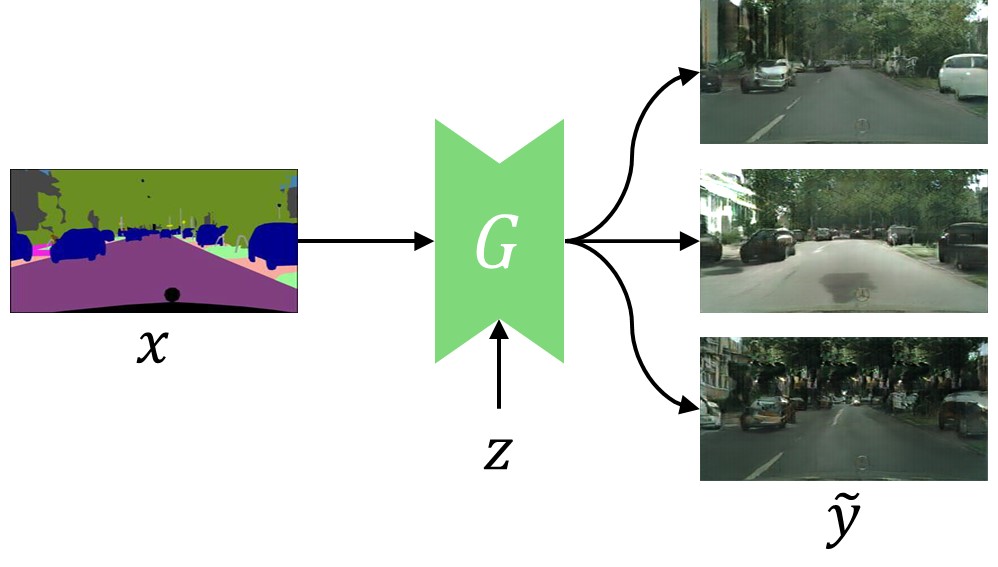
Desired one-to-many mapping

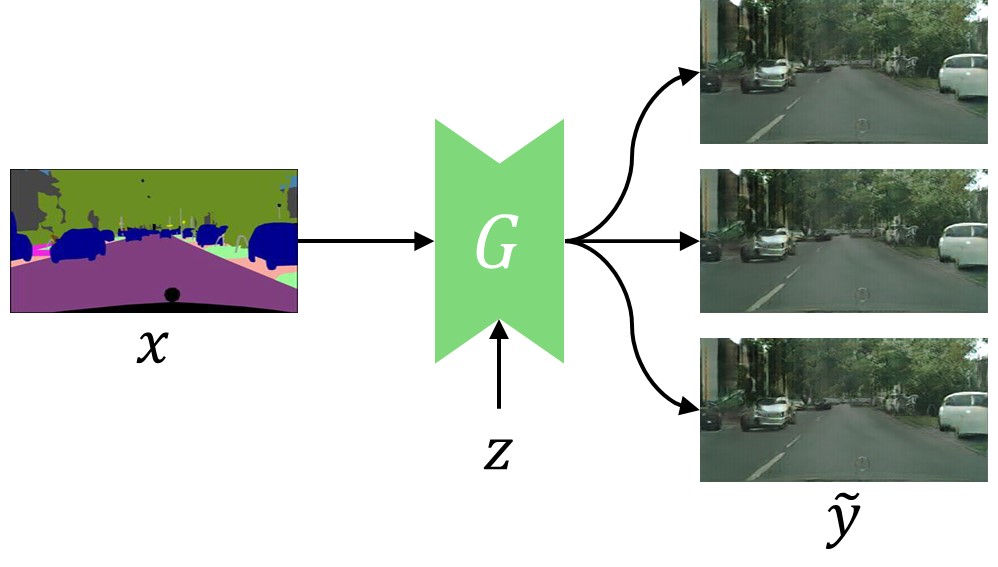
Mode collapse
(one-to-one mapping)

The following are excerpts from Isola et al. (2017), the original image-to-image translation paper.

… the generator simply learned to ignore the noise … Designing conditional GANs that produce stochastic output is an important question left open by the present work.

This phenomenon occurs in a variety of areas using conditional GANs. Consequently, almost every large-scale conditional GAN model omits random noise source.

The Origin of Reconstruction Loss

Due to the large instability of GAN training, reconstruction loss is an essential ingredient for training conditional GANs. The most common reconstruction losses in conditional GAN literature are the $\ell_1$ and $\ell_2$ loss. Both losses can be formulated as follows with $p=1,2$ respectively.

$$ \mathcal{L}_{\mathrm{Rec}} = \mathcal{L}_p = \mathbb{E}_{x, y, z} [ \|y - G(x,z) \|_p^p] $$

These two losses naturally stem from the maximum likelihood estimations (MLEs) of the parameters of Laplace and Gaussian distribution. Assuming a Gaussian distribution parameterized by mean $\mu$ and variance $\sigma^2$, the likelihood of a dataset $\mathcal{D}$ is defined as follows.

$$ \begin{align} P(\mathcal{D} | \mu, \sigma^2) &= \prod_{i=1}^N P(x_i | \mu, \sigma^2) \\ &= \prod_{i=1}^N \frac{1}{\sqrt{2\pi\sigma^2}} \exp \bigg(- \frac{(x_i - \mu)^2}{2\sigma^2} \bigg) \end{align} $$

Finding the maximum likelihood estimation of $\mu$ yields $\ell_2$ loss:

$$ \begin{align} \hat\mu_{\mathrm{MLE}} &= \argmin_\mu -\log P(\mathcal{D} | \mu, \sigma^2) \\ &= \argmin_\mu \sum_i^N \frac{(x_i - \mu)^2}{2\sigma^2} + \frac{1}{2} \log \sigma^2 + C \\ &= \argmin_\mu \sum_i^N (x_i - \mu)^2 \end{align} $$

We can also extend $\ell_2$ loss to find both mean and variance:

$$ \begin{align} \hat\mu_{\mathrm{MLE}}, \hat\sigma^2_{\mathrm{MLE}} &= \argmin_{\mu, \sigma^2} \sum_i^N \frac{(x_i - \mu)^2}{2\sigma^2} + \frac{1}{2} \log \sigma^2 \end{align} $$

Mismatch of Loss Functions in cGANs

The total loss function for the generator consists of two terms: the GAN loss and the reconstruction loss.

$$ \mathcal{L}_G = \mathcal{L}_{\mathrm{GAN}} + \mathcal{L}_{\mathrm{Rec}} $$

However, as we mentioned earlier, the $\ell_2$ loss is obtained in the process of finding the maximum likelihood estimation of the mean, not generating samples. We can decompose $\ell_2$ loss to see what $\ell_2$ loss is actually doing.

$$ \begin{align} \E_{y, \hat y} [(\tilde{y} - y)^2] =& \underbrace{\E_y \big[(y - \E[y])^2\big]}_{\textrm{Noise in data}} \\ +& \underbrace{\E_y \big[(\E[\hat y] - \E[y])^2\big]}_{\textrm{Output bias}} + \underbrace{\E_{y, \hat y} \big[(\hat y - \E[\hat y])^2\big]}_{\textrm{Output variance}} \end{align} $$

The $\ell_2$ loss is minimized when the two reducible terms, i.e. the output bias and variance, are zero. Let’s take a simple Gaussian as an example. As shown below, the optimal output distribution for the GAN loss is identical to the real data distribution. On the other hand, when the $\ell_2$ loss is used, the model should consistently output the exact mean of the distribution so that the output bias and variance are zero.

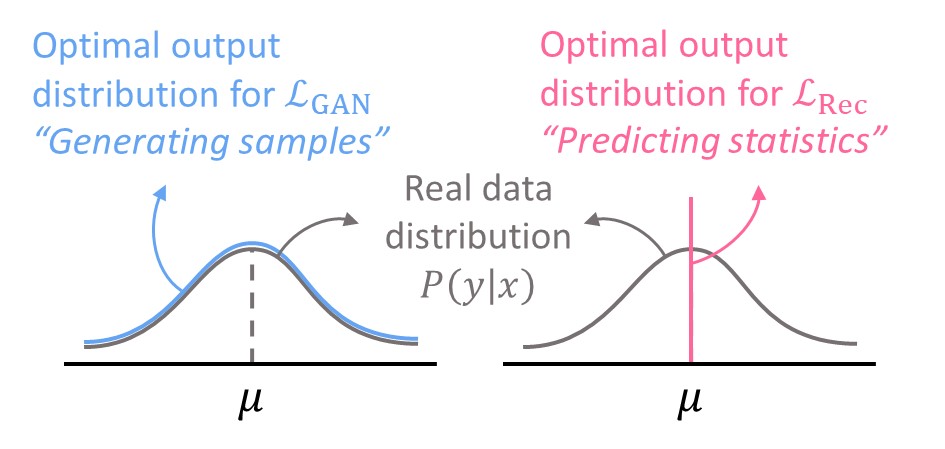
Mismatch between GAN loss and $\ell_2$ loss

In short, the generator cannot be optimal for both GAN loss and reconstruction loss!

The following animations show how the reconstruction loss ruins the GAN training. We use Y-shaped multimodal toy data and train a 2-layer MLP. The model takes an x-coordinate and a Gaussian random noise as input to output y-coordinate. Since the data is so simple, even GAN loss alone is enough to capture the data distribution. On the other hand, the $\ell_2$ loss shows a completely different pattern as expected: predicting the conditional mean of $y$. The combination of the two losses results in a complex dynamics. The individual samples are fairly close to real samples, but the model fails to capture the full distribution, i.e. mode collapse. Our loss, which will be presented in the next section, can greatly stabilize the GAN training without such side effects.

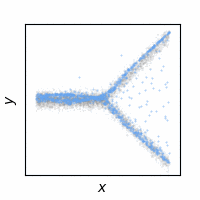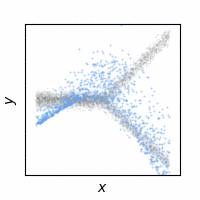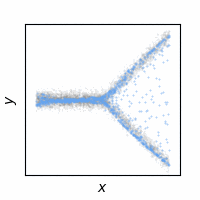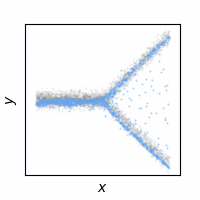
GAN

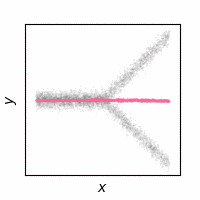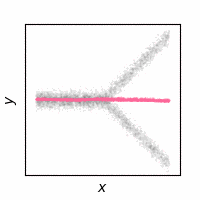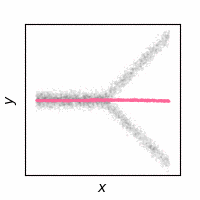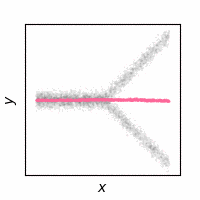
$\ell_2$

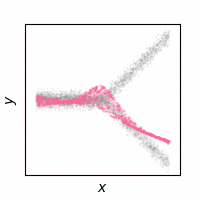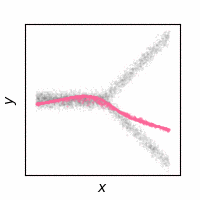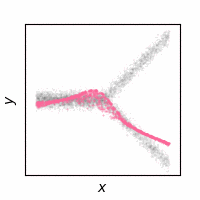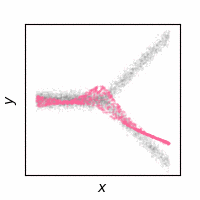
GAN + $\ell_2$

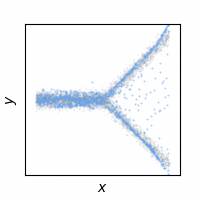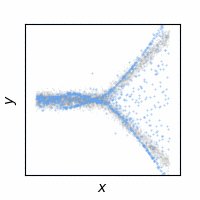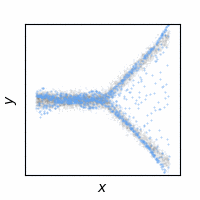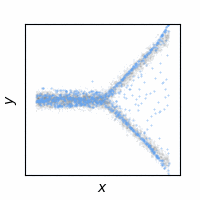
GAN + Ours

Approach

We propose novel alternatives for the reconstruction loss that are applicable to virtually any conditional generation tasks.

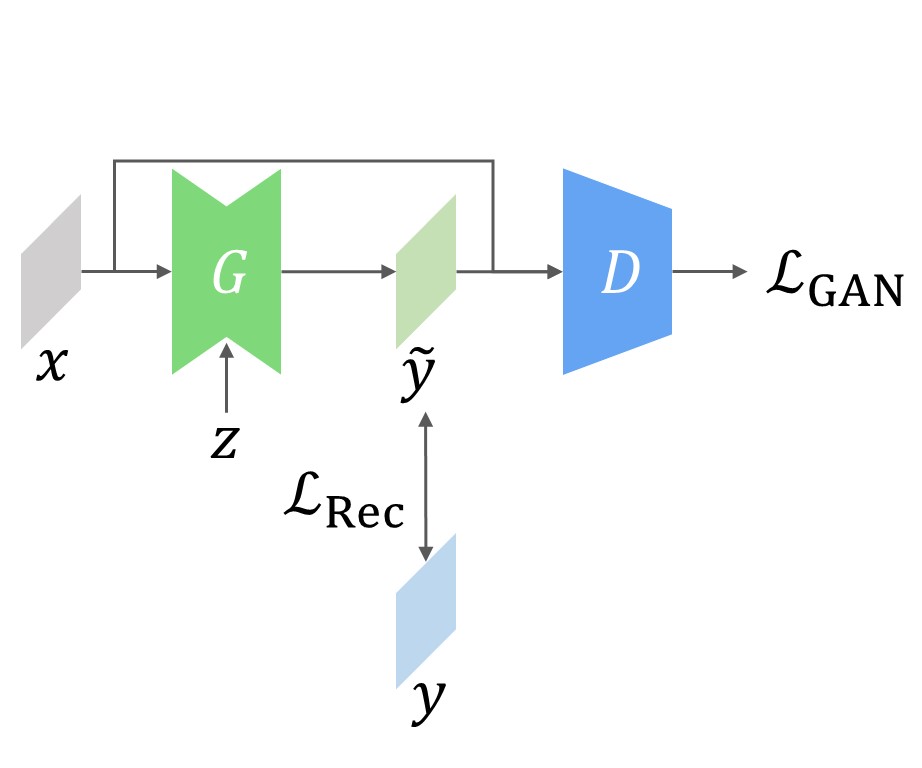
Conditional GAN

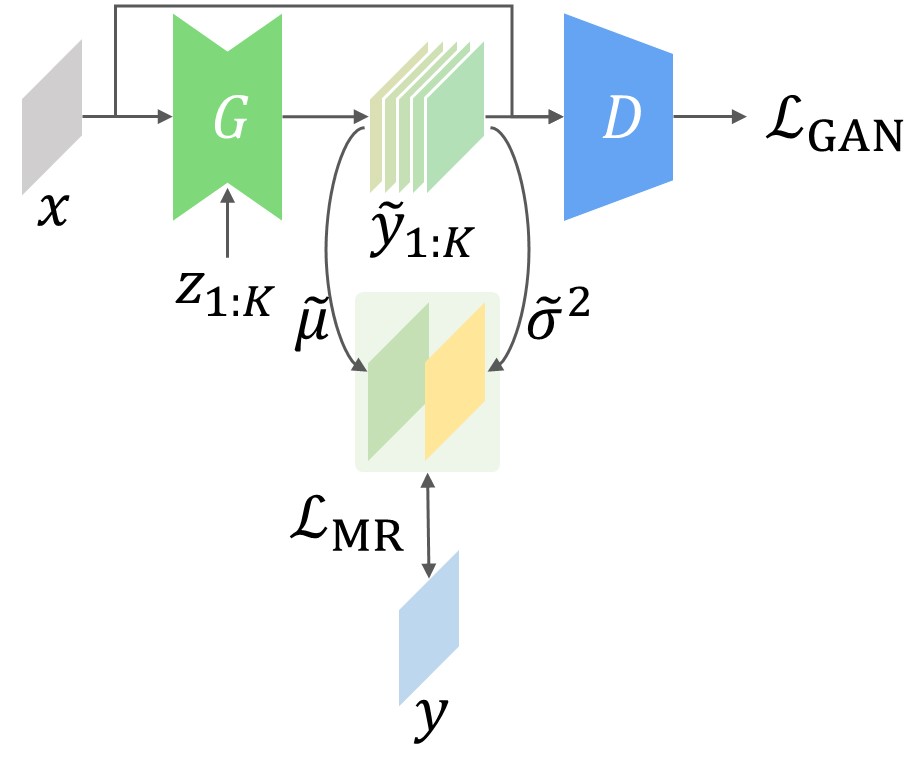
MR-GAN

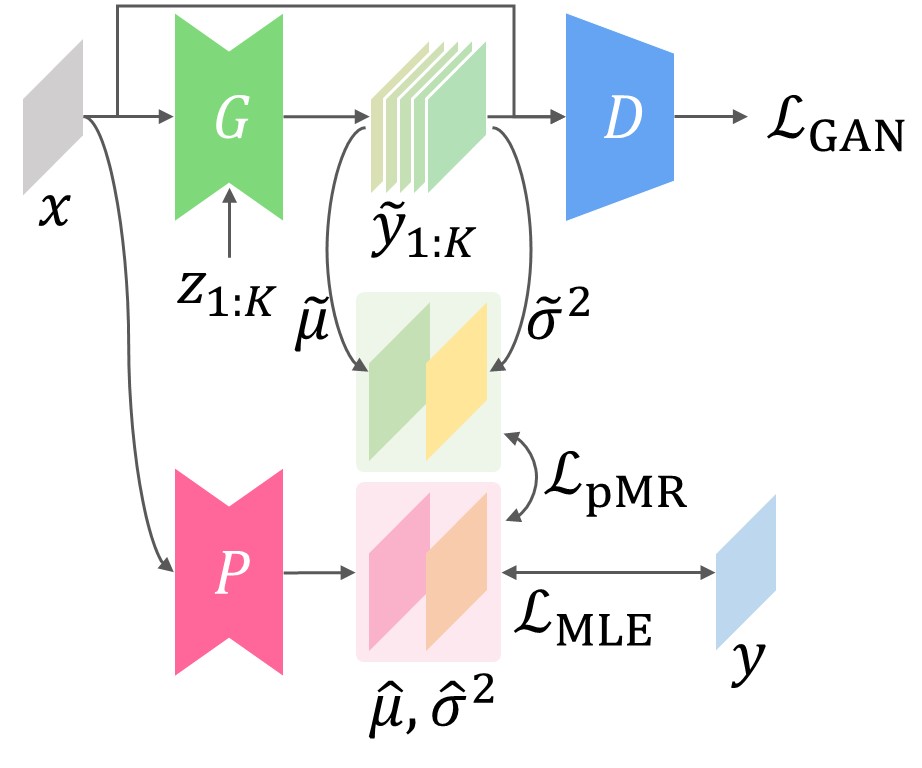
proxy MR-GAN

Moment Reconstruction Loss

Our first loss function is named Moment Reconstruction (MR) loss, and we call a conditional GAN with the loss as MR-GAN. There are two important differences from cGANs:

The generator produces $K$ samples for each input by varying the noise, i.e. $\tilde y_{1:K} = G(x, z_{1:K})$.
The MLE loss is applied to the sample moments (mean and variance).

Depending on the number of moments used, we define two versions of MR loss denoted MR$_1$ and MR$_2$.

$$ \begin{align} \Ls_{\mathrm{MR_1}} &= \E_{x,y} \big[ |y-\tilde{\mu}|^2 \big] \\ \Ls_{\mathrm{MR_2}} &= \E_{x,y} \bigg[ \frac{(y - \tilde\mu)^2}{2\tilde\sigma^2} + \frac{1}{2} \log\tilde\sigma^2 \bigg] \\ \textrm{where} \\ \tilde\mu &= \frac{1}{K} \sum_{i=1}^K \tilde y_i, \\ \tilde\sigma^2 &= \frac{1}{K-1} \sum_{i=1}^K (\tilde y_i - \tilde\mu)^2 \end{align} $$

Notice the similarity between the MR$_1$ loss and the $\ell_2$ loss. Since the generator is supposed to approximate the real distribution, we can regard that the moments of the generated distribution estimate the moments of the real distribution. Therefore, we apply the MLE loss on the sample moments, which fits the purpose of the MLE loss. This is a subtle but critical difference that makes our loss functions coexist with GAN loss in harmony.

Proxy Moment Reconstruction Loss

One possible drawback of the MR loss is that the training can be unstable at the early phase, since the irreducible noise in $y$ directly contributes to the total loss. For more stable training, we propose a variant called Proxy Moment Reconstruction (proxy MR) loss. The key difference is the presence of predictor $P$, which is a clone of the generator with some minor differences:

No noise source as input
Prediction of both mean and variance

Before training the generator, we train the predictor to predict the conditional mean and variance ($\hat\mu$ and $\hat\sigma^2$). Then we define the proxy MR loss as the sum of squared errors between predicted statistics and sample statistics:

$$ \begin{align} \Ls_{\mathrm{pMR}_1} &= (\tilde \mu - \hat \mu)^2 \\ \Ls_{\mathrm{pMR}_2} &= (\tilde \mu - \hat \mu)^2 + (\tilde \sigma^2 - \hat \sigma^2)^2 \\ \mbox{ where } &\hat\mu, \hat\sigma^2 = P(x). \end{align} $$

Similar to MR loss, proxy MR loss is divided into proxy MR$_1$ and proxy MR$_2$ according to the number of moments used.

Experiments

Comparison of Loss Configurations

We train a Pix2Pix variant, which has random noise source, on Cityscapes dataset with different loss configurations. For each configuration, we present four samples generated from different noise inputs.

Input

Ground truth

(a) GAN

(b) $\ell_1$

(d) GAN + Ours

(a) Using the GAN loss alone is too unstable to learn the complex data distribution.
(b) Using the $\ell_1$ loss only, the model generates blurry images, which is the conditional median of real-image distribution given the input.
(c) The combination of the two losses enables the model to generate visually appealing samples but results in serious mode collapse.
(d) The model trained with our loss term (proxy MR$_2$) generates a diverse set of images without losing visual fidelity.

The Generality of Our Methods

In order to show the generality of our methods, we conduct experiments on three conditional generation tasks with three cGAN models:

Image-to-image translation: Pix2Pix–Maps
Super-resolution: SRGAN–CelebA
Image inpainting: GLCIC–CelebA

In every tasks, our methods successfully generate diverse images as presented below.

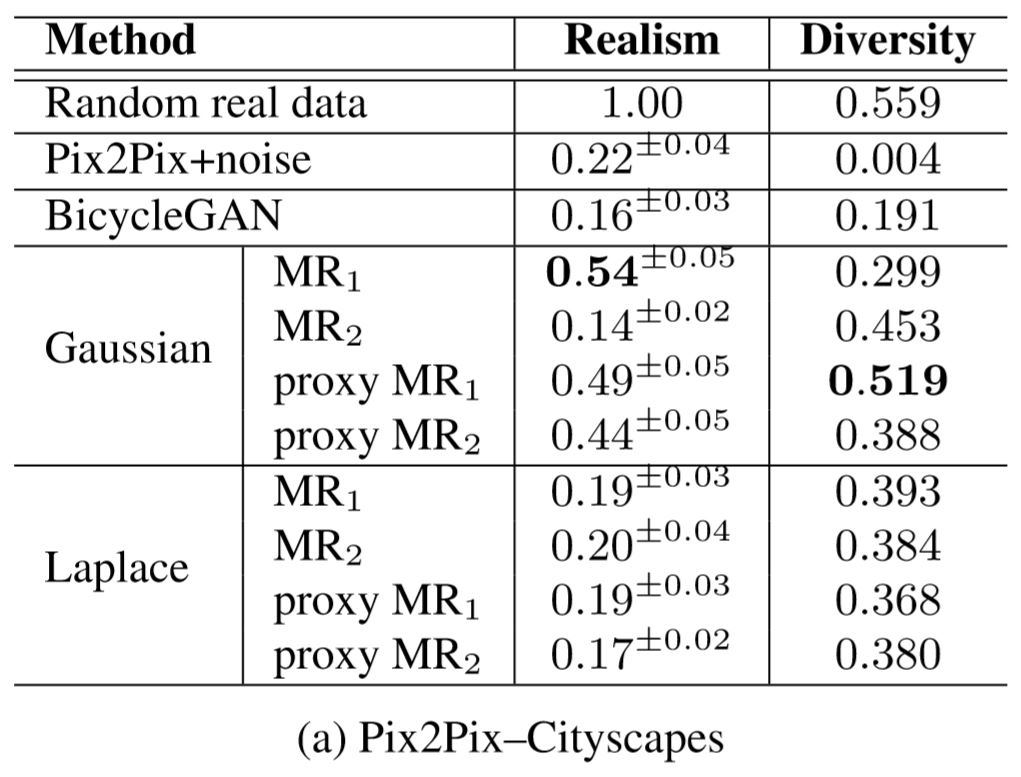
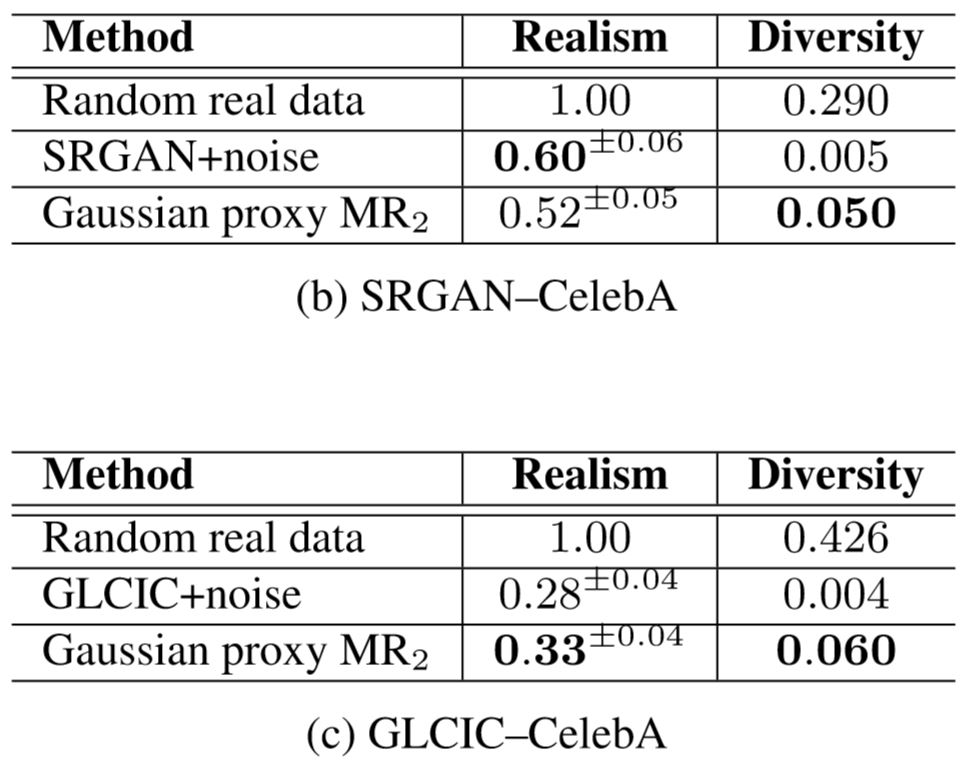
Quantitative Evaluation

For comparison, we quantitatively measure the diversity and realism on three method–dataset pairs. We use LPIPS score for diversity and human evaluation score for realism. Specifically, we use $2(1-F)$ for realism where $F$ is the averaged F-measure of identifying fake by human evaluators. In all three tasks, our methods generate highly diverse images with competitive or even better realism.

Reference

If you are willing to cite this paper, please refer the following:

@inproceedings{
    lee2019harmonizing,
    title={Harmonizing Maximum Likelihood with {GAN}s for Multimodal Conditional Generation},
    author={Soochan Lee and Junsoo Ha and Gunhee Kim},
    booktitle={International Conference on Learning Representations},
    year={2019},
    url={https://openreview.net/forum?id=HJxyAjRcFX},
}

Acknowledgement

We especially thank Insu Jeon for his valuable insight and helpful discussion. This work was supported by Video Analytics CoE of Security Labs in SK Telecom and Basic Science Research Program through National Research Foundation of Korea (NRF) (2017R1E1A1A01077431). Gunhee Kim is the corresponding author.